Richtig gerechnet, falsch gedacht
 

Schon auf der Schule lernt man den Unterschied zwischen Fächern, in denen man schwafeln kann, um Lorbeeren zu ernten, und anderen Fächern, in denen das nicht möglich ist. Letztere gelten nicht nur als schwerer zu erlernen, sondern auch als wesentlich solider in ihren Resultaten. Die Ökonomie ist solch ein Fach, und das soll sie dem Gebrauch der Mathematik verdanken.

A. Das falsche Lob der Mathematik

Durch die Verwendung von Mathematik soll ein Ding namens „exakte Wissenschaft“ zustande kommen. Bloß: Was ist eine exakte Wissenschaft? An und für sich eine pure Tautologie. Genauso wie „weißer Schimmel“ oder „alter Greis“. Denn Wissenschaft besteht darin, gerade die Bestimmungen einer Sache zu erschließen und in Urteile zu fassen, die ihr und nicht irgend etwas anderem zukommen.

Deshalb erfährt man auch nie, was denn eine Wissenschaft wäre, die nicht exakt vorginge, und was sie insofern für Fehler machte. Statt dessen bekommt man jede Menge Vorteile des Gebrauchs der Mathematik aufgezählt:

l. Zahlen sind genau

Ebenso oft sind sie natürlich ungenau. Bekannte Frage: Wie viele Stellen nach dem Komma sollen es denn sein? Genauigkeit ist keine den Zahlen immanente Eigenschaft, sondern eine an sie genauso wie an andere Bestimmungen einer Sache zu stellende Forderung.

Beispiel:

I. Freifallende Körper erfahren eine Beschleunigung von 9,8l m/s².

II. Demokratien sind Rechtsstaaten.

Das zweite Beispiel haben wir natürlich heimtückischer Weise so gewählt, dass keiner die Wahrheit dieses Urteils bestreiten wird. Aber selbst wenn dem so wäre: dann würde so ein Zweifler gerade genau wissen, was wir gesagt haben und er nicht für richtig hält.

Irgendein Unterschied in der Genauigkeit beider Aussagen ist offenbar nicht zu entdecken. Mehr noch: jeder Versuch, Aussage II durch Zahlen präziser und schärfer zu machen, ist albern, geht völlig an der Sache vorbei. Was wollte man denn hier zählen? Gesetze, Polizisten, Gerichtsverfahren, Strafgefangene? Davon gibt es in „Unrechtsregimes“ genauso viel. Und um den Vergleich vollständig zu machen, stelle man sich einmal vor, was in beiden Sachgebieten eine ungenaue Aussage wäre:

I. Die Beschleunigung ist ziemlich groß.

II. In der Türkei gibt es wieder beinahe rechtsstaatliche Verhältnisse.

In beiden Fällen weiß man nicht, woran man ist; das wird zur Standpunktfrage. Bei I. wird das in der Natur der hier gegebenen Bestimmung (groß) liegende Bedürfnis nach Zahlenwerten nicht befriedigt. Es wird von Größe geredet, aber diese nicht angegeben. Bei II. wird eine Bestimmung angegeben, von der zugleich gesagt wird, dass sie nicht zutrifft. Genauso gut könnte man sagen: In der Türkei herrscht keine ordentliche Diktatur mehr.

2. Zahlen sind objektiv

Hier können wir nur unsere Argumentation von oben wiederholen. Es ist nicht zu sehen, wieso II. weniger objektiv als I. sein soll, oder wie man II. objektiver machen könnte. Schlaumeier werden aber vielleicht noch einwenden, dass sich Zahlen immerhin objektiv ermitteln lassen. „Objektiv“ soll hier also heißen, dass es Messapparaturen und -verfahren gibt, die ganz unabhängig von den Wünschen und Meinungen der Subjekte die in Frage stehenden Größen feststellen, während eine ähnlich Vertrauen erweckende „übersubjektive“ Prozedur für „qualitative“ Aussagen nicht zur Verfügung stehe. Bloß: Eben waren doch noch alle einig, dass Demokratien Rechtsstaaten sind, und das ganz ohne Messgeräte. Und, noch viel wichtiger: Wenn man irgendeine Größe messen will, sagen wir die Temperatur, muss man doch zuallererst wissen, um was es überhaupt geht. Denn das ist nicht möglich: objektive Zahlen für die Temperatur gewinnen und es für sehr subjektiv halten, was eine Temperatur ist, ob eine solche vorliegt, wie sie erfasst werden kann etc. Man braucht eine ganze Theorie, bevor man Thermometer bauen kann. Der Blödsinn dieser Vorstellung ist also, dass man seinem Verstand weniger trauen möchte als einem technischen Gerät, das als Hilfsmittel der Erkenntnis fungiert. Bloß: Dieses Gerät selbst, genau wie sein zweckmäßiger Gebrauch, ist eine Leistung des Verstandes. Das ist bekanntlich der Unterschied zwischen Messgerät und Wünschelrute.

3. Die Sprache der Mathematik ist eindeutig

Bekanntlich versteht sie deshalb auch kein Schwein. Wenn irgendwo im Mathematikbuch steht

^d/_dx tan x = 1/ cos²x   ;

dann ist das dasselbe wie der gute deutsche Satz

„die erste Ableitung der Tangensfunktion ist gleich dem Kehrwert des Quadrats der Cosinusfunktion.“

Weil beide Versionen haargenau dasselbe besagen, ist keine eindeutiger als die andere. Der Gebrauch von Symbolen schafft nicht die Eindeutigkeit von Begriffen und Gedanken, sondern setzt sie voraus; um eine Notation wie d/dx sinnvoll gebrauchen zu können, muss ich wissen, was die Ableitung einer Funktion ist. Und wenn ich davon keine Ahnung oder nur nebelhafte Vorstellungen habe, hilft mir das Symbol nicht weiter. Das ist in der Mathematik nicht anders als im wirklichen Leben. Man denke z.B. an die Verkehrszeichen: Wer nicht weiß, was „anhalten und warten“ ist, kann mit dem Rotlicht einer Ampel nichts anfangen. Man denke auch an den üppigen Gebrauch von Symbolen in Pseudowissenschaften: Astrologie, Alchimie, Magie: Hier sind Symbole Vehikel der Scharlatanerie.

Eine ganz andere Frage ist es, dass man seine Gedanken durch die Sprache, aber auch durch Symbole, unvollkommen, etwa mehrdeutig ausdrücken kann. Dann muss eben zurückgefragt werden, ein paar zusätzliche Sätze sind fällig etc. Alle Beispiele dafür, wie man durch den Gebrauch der Sprache in die Irre geführt werden kann („Der Herr traf die Dame mit dem Regenschirm.“), belegen gerade nicht, wie sie wollen, einen grundsätzlichen Mangel der Sprache. Um dem Leser mitzuteilen, was das Missverständnis ist, muss ihm nämlich auch noch schnell das richtige Verständnis mitgeteilt werden; und siehe da: Das ist machbar! Im übrigen sollten sich die Freunde der mathematischen Symbolsprache mal folgendes vor Augen halten. Es gibt kaum ein Symbol, das so viele verschiedene Bedeutungen hat wie das x der Mathematiker. In jedem Kapitel eines Buchs, in jedem Buch eine andere. Sogar in der oben genannten Formel wird x in zweifachem Sinn verwendet: In Ausdrücken wie tan x kann ich Zahlen für x einsetzen, z.B. tan 0. Aber dies kann ich bei dx gerade nicht tun, und deshalb auch nicht bei dem Gesamtausdruck.

Zusatz: Dass Mathematiker Symbole benutzen, hat praktische Gründe. Diese sind bequemer zu benutzen als die entsprechenden Wortungetüme, und wenn Mathematiker sich etwas zu sagen haben, dann Stellen sie sich vor eine Tafel. Dass sie überhaupt so komplizierte Ausdrücke brauchen, kommt daher, dass sie mit ihren Gegenständen operieren müssen Bildung des Kehrwerts, des Quadrats etc. Und solches Operieren lässt sich eben sehr gut durch das Zusammenstellen von Symbolen zu einer Formel ausdrücken; man kann damit dann auch gleich rechnen. Dasselbe gilt übrigens für die Formeln der Chemie.

4. Die Mathematik ist logisch

Dass in der Mathematik keine Fehlschlüsse vorkommen können, wird wohl niemand behaupten, der sich einmal ernsthaft um die Materie bemüht hat. Wenigstens an seinen eigenen Bemühungen gewinnt er ganz schnell Beispiele dafür, wie leicht man auch hier Fehler machen kann. Und die Geschichte der Mathematik ist voll davon. Eine andere Sache ist es, dass Mathematiker sehr viel Wert darauf legen, dass ihre Sachen stimmen; insbesondere lassen sie nichts ohne Beweis durchgehen. Aber bitteschön: Was sollte denn andere Wissenschaften davon abhalten, auf ihrem Gebiet ebenfalls auf richtigen Schlüssen und Beweisen zu bestehen? Und im übrigen sind diese Dinge noch nicht einmal Spezifika der Wissenschaft, sondern an der Tagesordnung, seit die Menschheit das Neandertal verlassen hat. Schon die Kinder wissen, wann etwas „logo“ ist. Gemeint ist mit diesem Lob der Mathematik wieder eine ziemlich krumme Vorstellung. Nämlich dass sich die Argumente der Mathematiker überprüfen ließen, und zwar nicht so, dass man sie nachvollzieht, also mitdenkt. Sondern so, dass man die Richtigkeit eines Beweises feststellen könne, ohne sich auf seinen Inhalt einzulassen: ganz „formal“, und daher „objektiv“. Das geht weder in der Mathematik noch sonstwo. Denn was da verlangt wird, ist ein Widerspruch: man soll richtig denken, ohne etwas zu denken, also ohne überhaupt zu denken.

Formale Richtigkeit - ein Unsinn

Die Vorstellung, dass dieses falsche Ideal formaler Richtigkeit wenigstens in der Mathematik praktiziert werden könne, pflegt sich auf einen weiteren Unsinn zu berufen. Nämlich dass die Mathematik keine Gegenstände und Inhalte habe. Bloß: Womit befassen sich denn die Mathematiker dauernd? Die Theorie der Differentialgleichungen zum Beispiel befasst sich mit den Differentialgleichungen. Was denn sonst! Und dass Differentialgleichungen keine Kohlköpfe sind und keine politischen Systeme, heißt noch lange nicht, dass sie nichts wären; sie sind eben etwas anderes. Und wenn jetzt einer wissen will, was es mit diesen Differentialgleichungen auf sich hat können wir ihm bloß raten, die einschlägige Theorie zu studieren.

Wissenschaftliche Willkür feiert die Mathematik als ihr Hilfsmittel

Die Gründe, die für den Gebrauch der Mathematik angeführt worden sind, sind samt und sonders nicht stichhaltig. Ihnen gemeinsam ist der Wunsch. in der Mathematik ein Mittel zu haben, das anständige wissenschaftliche Ergebnisse garantiert, also von sich aus und automatisch dafür sorgt, dass richtige Urteile zustande kommen und Fehlschlüsse vermieden werden. Bloß: Wenn man richtige Ergebnisse haben will, ist es doch überhaupt nicht klar, ob die Mathematik dabei im konkreten Fall auch nur die geringste Hilfestellung bietet. „Richtig“ heißt doch, wir sprachen eingangs schon davon, dass die Ergebnisse tatsächlich Bestimmungen der untersuchten Sache sind, dass sie zutreffen, also spezifisch sind. Und warum sollte eine x-beliebige Sache ausgerechnet mathematische Bestimmungen haben? Umgekehrt: Wenn ein Wissenschaftler sich - beispielsweise aus den oben betrachteten Gründen - dazu entschließt, auf seinen Forschungsgegenstand mit mathematischen Methoden loszugehen, dann leistet er sich ein Vorurteil. Denn diese Wahl der Methode begründet sich nicht aus seiner Kenntnis der Sache, sondern soll ihm, wie er selbst versichert, erst zu solchen Erkenntnissen verhelfen. Er fängt also die Wissenschaft damit an, dass er festlegt, wie seine Resultate aussehen sollen - und das ausgerechnet zu dem Zweck, solche Ergebnisse erst zu kriegen.

Die Mathematik wird auf diese Weise das Gegenteil von dem, was sie angeblich ist. Sie dient nicht als Instrument größerer Exaktheit, sondern als ein Medium, in dem der Forscher ausdrückt, wie er die betrachteten Gegenstände sehen will. Am Anfang steht so die Willkür: Sowenig es klar sein kann, dass sich der Untersuchungsgegenstand überhaupt mathematisch erfassen lässt, sowenig ist klar, was für mathematische Qualitäten ihm im einzelnen zugeschrieben werden können. Das ist also eine Frage des Interesses eines solchen Wissenschaftlers; er entscheidet, dass und wie er eine Sache als Größe, als Funktion usw. sehen will. Die Objektivität der Wissenschaft ist somit beim Teufel, bevor sie überhaupt angefangen hat. Und was dann nach solchen Ansätzen kommt, macht die Gesamtveranstaltung auch nicht besser: Da beschäftigt man sich fleißig mit dem Material, um seine sehr subjektiven Ausgangsvorstellungen mit Leben zu erfüllen.

Übrigens: Hartgesottene Vertreter dieser Willkür in der Wissenschaft wollen die Sache mit der Exaktheit dann auch lieber sehr viel enger verstanden wissen. Die Mathematik soll diesen Skeptikern zufolge nicht mehr zur Richtigkeit der Theorie beitragen, sondern lediglich helfen, die Hypothesen, die man sich frei und nach Belieben ausdenkt, „stimmig“ und „wasserdicht“ zu formulieren. Diese Vorstellung grenzt nun aber wirklich schon an Idiotie: Richtig sollen die eigenen Gedankenkonstrukte nicht sein, aber in sich stimmig. Im Ernst: Warum machen solche Freunde subjektiver Geistesfrüchte nicht die Auflage, dass dieselben in Gedichtform, in Hexametern oder sonstwie streng geregelt in die Welt gesetzt werden?

Im Folgenden soll an drei Beispielen gezeigt werden, was für unwissenschaftliche Betrachtungsweisen Volkswirte produzieren, wenn sie sich so ganz exakt ans Werk machen. Dabei wird sich auch ein Einwand von selbst erledigen, den mancher Leser vielleicht jetzt noch hat. Der Einwand nämlich, dass mit dem Entschluss zur Mathematik noch „nicht viel“ gesagt sei. Diesbezüglich sei vorerst nur an zweierlei erinnert. Erstens soll nach allgemeiner Meinung doch mit der Mathematik „furchtbar viel entschieden sein, nämlich der wissenschaftliche Charakter der ganzen Veranstaltung. Und zweitens ist es eben einfach nicht wahr, dass die Mathematik „nichts“ ist. Sie handelt zum Beispiel von Quantitäten und deren Gesetzen, und unser erstes Beispiel wird gleich zeigen, wie sehr man die Welt und seinen eigenen Verstand vergewaltigen muss, um ökonomische Größen zu entdecken, die gar nicht da sind.

B. Drei Beispiele

Beispiel l: Das Sozialprodukt oder die Wirtschaft als Zahl

Das Sozialprodukt kennt heute jeder; es steht mindestens so oft in der Zeitung wie der Bundeskanzler. Denn es handelt sich um die „wichtigste Kennziffer des Wirtschaftsgeschehens“.

Bloß: Wieso soll es denn überhaupt eine Größe geben, die ausdrückt und zusammenfasst, was wirtschaftlich los war während eines Jahres die also die Ökonomie insgesamt zu charakterisieren imstande ist. Auch wenn es bei mancherlei technischen Dingen - vom Wechselstrom bis zur Benzinqualität - solche Kennziffern gibt, ist deren Existenz keine Selbstverständlichkeit, die überall zuträfe. Schließlich gibt es auch keine Zahlen, die überzeugend auszudrücken vermöchten, wie etwa die weltpolitische Situation oder der Geisteszustand der Menschheit beschaffen ist.

Wie kommt also ein Ökonom auf die gewünschte wirtschaftliche Kennziffer? Leider so, dass ihm der Wunsch als Vater aller weiteren Gedanken völlig ausreicht. Hier wird also nicht die Wirtschaft analysiert und dabei eine Größe entdeckt, auf die es wesentlich ankommt. Sondern hier wird umgekehrt und sehr willkürlich ein Gesichtspunkt konstruiert, der die angestrebte Quantifizierung zu liefern verspricht.

„Wir betrachten die gesamte Volkswirtschaft - modellhaft vereinfacht - als eine einzige Riesenunternehmung, die durch einen Kasten dargestellt wird, von dem wir zunächst nicht wissen (wollen) was in seinem Inneren vor sich geht. Auf der einen Seite geht ein Input ein und auf der anderen Seite kommt in einer Periode (zum Beispiel in einem Jahr) durch die Produktion m der Riesenunternehmung Volkswirtschaft ein Output heraus. Hinsichtlich des Output nehmen wir zunächst in extremster Abstraktion an, dass nur ein einziges Universalgut hergestellt wird, das sich für alle denkbaren Verwendungszwecke gleich gut eignet. Wir wollen das Gut Sozialprodukt nennen.“ (Bartling-Luzius, 22)

Gegen diese Definition des Sozialprodukts ist nun nicht einzuwenden, dass die Realität zu sehr „vereinfacht“ und in diesem Sinne "abstrakt" dargestellt wird. Sondern dass hier zu einem ganz verkehrten Gedanken aufgefordert wird. Man soll sich eine Vorstellung von der Wirtschaft machen - aber ausdrücklich ohne etwas von ihr wissen zu wollen. Drastischer kann man die Unwissenschaftlichkeit dieses `Vorhabens nicht charakterisieren. Aber weil das so schlecht geht - sich eine Wirtschaft zurechtphantasieren, aber immerhin noch eine Wirtschaft -, wird explizit angegeben, wo man lügen muss Man soll so tun, als ob ein Universalgut hergestellt würde. Man soll also das was zu beweisen wäre, nämlich dass die Wirtschaft eine einheitliche und insofern bezifferbare Leistung hat, einfach mal voraussetzen, und das sogar trotz eingestandenen Widerspruchs zur Realität.

Man sieht hier, wie das Ideal mathematischer Exaktheit die Ökonomen dazu treibt, sich höchst unexakte Gedanken zu machen. Der Einfall, die Wirtschaft in eine Zahl zusammenzufassen, hat die Ökonomen auf den Blödsinn eines Universalgutes gebracht, und dieses Universalgut wird sie jetzt zu weiteren drolligen Bocksprüngen veranlassen. Denn die Frage, wieviel Universalgut alias Sozialprodukt herauskommt, ist ja eben deshalb alles andere als leicht zu beantworten, als dieses schöne Universalgut ganz gewiss weder von VW noch von Maggi produziert wird.

Die übliche Ausflucht ist nun, einfach jedes Gut, es mag sein, was es will, als ein Stück Universalgut zu betrachten. Das Sozialprodukt „stellt die Summe aller Güter und Dienstleistungen dar“ (Henrichsmeyer, 247). Nun bringt diese glückliche Antwort auf die Existenzfrage des Sozialprodukts - einfach festzulegen, dass alle Güter und Dienstleistungen zusammen dieses Universalgut darstellen - wieder die allergrößten Probleme mit sich:

Problem Nr. 1 ist, wie es so schön heißt, technischer Natur.

„Will man zu Gesamtgrößen für eine Volkswirtschaft gelangen, so versagt das Verfahren, mit Hilfe physischer Mengeneinheiten zu messen, völlig. Es muss dann eine allen Gütern gemeinsame, Messbare und additive Eigenschaft gefunden werden.“ (Stobbe, 285)

Man kann nicht Apfel und Birnen, Haarschnitte und Beerdigungen einfach zusammenzählen, um eine runde Summe zu erhalten. Hier wirkt sich die mathematische Exaktheit leider sehr störend aus. Zwar liefert sie einem die Vorstellung einer Summe (gut!), aber leider auch ein paar Rechenregeln dazu (schlecht). (Wir erinnern hier an die gutwillige Meinung, dass mit der Übernahme mathematischer „Denkformen“ noch „nichts entschieden“ wäre. Eben doch! Um den ganzen Plunder, der in der Ökonomie vorkommt, unter die Vorstellung einer mathematischen Summe zu subsumieren, müssen, eben weil eine Summe auch etwas Bestimmtes ist und ihre eigenen Gesetzmäßigkeiten hat, schon noch ein paar Anpassungen vorgenommen werden.)

Problem Nr. 2 ist die heiße Frage, was alles in diesen Summationsprozess eingehen kann und darf.

Gerade weil die Wirtschaft weder eine Riesenunternehmung noch überhaupt ein schwarzer Kasten ist, ist völlig offen, was man als ihren Output ansehen soll. Gehören Apfel und Birnen dazu? Klar. Haarschnitte und Beerdigungen? Dito. Aber wie steht es mit Herbstmanövern und Bundestagsreden? Oder was ist mit Teach-ins oder Flugblättern der MG? Sicherlich alles „produzierte“ Dinge und sicherlich auch alles „nützlich“, zumindest in den Augen dessen, der sie produziert. Angesichts dieser doppelten Schwierigkeit entschließt sich die wissenschaftliche Ökonomie - und hier handelt es sich wirklich um einen Entschluss, um eine durch kein einziges sachliches Argument zu stützende Festlegung -, die Lösung wiederum mithilfe des Ideals mathematischer Exaktheit zu finden. Zahlen will man haben, und deshalb nimmt man einfach, was an Zahlen ohnehin existiert. Nämlich die Preise von Gütern und Dienstleistungen.

„Statt solcher technischen Attribute (Pfund Äpfel; Stück Beerdigung) verwendet man als die gesuchte Eigenschaft trotz aller damit verbundenen Nachteile die Marktpreise der Waren.“ (Stobbe, 285)

Das ist zwar nicht logisch, aber konsequent. Denn die Frage nach der zu messenden Qualität - also Bestandteil des gesamtwirtschaftlichen Outputs zu sein - wird hier ersetzt durch ein Messverfahren, das als einzigen Vorteil haben soll, durchführbar zu sein. Alles, was einen Preis hat, ist eben dadurch auch schon als Bestandteil des Sozialprodukts qualifiziert. Und das erledigt ganz en passant auch Problem Nr. l. Als Preise sind natürlich alle Güter aufsummierbar. Weil aber Preise nicht dazu gemacht werden, einem Ökonomen die Bildung des Sozialprodukts zu erleichtern - Preise sind eine praktische Angelegenheit, über sie macht der Warenbesitzer seinen Gewinn -, zeitigt diese saubere Lösung gleich eine Latte neuer Probleme. Zum Beispiel: Es gibt Dinge, die, weil nicht für Verkauf und Gewinn bestimmt, keinen Preis haben, aber von Ökonomen gern eingeschlossen würden, weil sie nach landläufiger Meinung mindestens so wertvoll sind wie alles was für Mark und Pfennig feilgehalten wird. Da gibt es das segensreiche Wirken des Staates, von den Autobahnen und Schulen bis zu den weniger fasslichen Gütern der Sicherheit oder der Ordnung. Oder da gibt es die tüchtige Hausfrau, die die Waschmaschine bedient, Äpfel im eigenen Garten erntet und jede Menge Mutterliebe verstreut. Zum Beispiel: Dass sich Preise verändern - und zwar ganz einfach deshalb, weil das Geld Gegenstand ökonomischer Interessen und kein Messgerät der Forschung ist -, ist dem Ökonomen Anlass zur Frage, ob denn die auf dem Markt anzutreffenden Preise wirklich wiedergeben, mit welchem Gewicht ein Produkt dem Sozialprodukt einzugliedern ist. Soll man die aktuellen Preise nehmen, oder sind die von l955 richtiger? Und wie berücksichtigt man, dass seitdem die Milch dünner und die Autos dicker geworden sind?

Zusammenfassung:

Das Streben nach mathematischer Exaktheit führt zu allergrößter Konfusion, Willkür und Streit. Und das eben deshalb, weil dieses methodische Ideal das Gegenteil einer anständigen wissenschaftlichen Befassung mit den Gegenständen ist. All die Sorgen um Messbarkeit, richtige Preise, statistische Prozeduren etc. bringen einen Ökonomen nie auf den einfachen Gedanken, dass er vielleicht etwas Falsches, eine nicht existente Größe zu ermitteln sucht. Vielmehr sieht er sich bestätigt darin, dass es eben nicht leicht sei, aber umso wichtiger, sich um Genauigkeit zu bemühen. Ganz unangezweifelt und eher noch bestärkt geht deshalb die ideologische Botschaft, der Inhalt des ganzen Rechenwerks, aus solchen Schwierigkeiten hervor. Die Botschaft nämlich, dass die Wirtschaft insgesamt genauso zu betrachten sei wie irgendein Produktionsprozess, den einer unternimmt, damit hinterher ein Produkt herauskommt.

Dieses falsche Dogma von der Wirtschaft als ertragbringender Veranstaltung erhält Glaubwürdigkeit dadurch, dass man es mathematisch fasst, also sich bemüht, die Größe des fiktiven Ertrags möglichst exakt auszurechnen.

Und angesichts dieser hochwissenschaftlichen Lüge gilt die schlichte Wahrheit als unwissenschaftlich, dass nämlich die Wirtschaft keine Gemeinschaftsveranstaltung ist, sondern sich durch Konkurrenz auszeichnet, und dass ihre Leistungen in dicken Profiten und massenhaftem Elend bestehen.

Beispiel 2: Die Einnahmen-/Ausgaben-Analyse oder die Wirtschaft als Punkt und Kurve

Am Beispiel des Sozialprodukts haben wir jetzt gesehen, wie der Makroökonom fiktive Größen in die Welt setzt. Genauso wie er sich beim Sozialprodukt vorstellt, dass die Wirtschaft insgesamt ein Ergebnis habe, so stellt er sich nun unter den Titeln gesamtwirtschaftliches Einkommen (Y) und gesamtwirtschaftliche Ausgaben (A) vor, dass die Wirtschaft insgesamt - so wie jeder Arbeiter, Kapitalist, Rentenempfänger - ein Einkommen und daraus zu tätigende Ausgaben habe. Zwischen diesen beiden Größen Y und A möchte er als nächstes eine Funktionsbeziehung entdecken. Die Verwandlung der Wirtschaft in ein Fabelreich von Größen, die als gesamtwirtschaftliche an keiner Stelle im Wirtschaftsprozess eine Rolle spielen können, ergänzt er um das Programm, eben diese Abstraktionen mit eigenem Leben zu erfüllen: nämlich sie als solche aufeinander einwirken oder voneinander abhängen zu lassen. Er möchte z.B. jetzt das gesamtwirtschaftliche Einkommen zum Grund dafür machen, dass die gesamtwirtschaftlichen Ausgaben so und so hoch sind:

„Die Formulierung solcher Hypothesen in der Form mathematischer Gleichungen nennt man Verhaltensgleichungen. Sie schildern die verhaltensbedingte Abhängigkeit der Zielgrößen von den jeweiligen Determinanten.“ (Münnich, 26)

Um sein wissenschaftliches Ziel, die eine makroökonomische Größe als durch die andere bestimmt darzustellen, plausibel zu machen, lässt er sich das Verhalten der Leute einfallen. Das ist schon komisch: Denn wie sollte sich irgendein lumpiges Wirtschaftssubjekt zu solchen Abstrakta wie Volkseinkommen und gesamtwirtschaftliche Ausgaben verhalten? Aber noch schlimmer: „Verhaltensbedingte Abhängigkeit des A von der Determinante Y“ heißt das widersprüchliche Programm. Hier müsste sich der Ökonom logischerweise entscheiden: Entweder ist das Verhalten der Leute dafür verantwortlich, was los ist auf der Welt, oder die eine Größe für die andere. Entweder ist das Wirtschaftssubjekt mit seinem Verhalten entscheidend für die Volksausgaben A. Oder die Ausgaben A sind bestimmt durch das Einkommen Y; dann ist das Wirtschaftssubjekt mit seinem Verhalten zu den Zielgrößen als bedeutungslos erklärt für den Zusammenhang von A und Y.

Schon die Bezeichnung „Verhalten“ ist verkehrt, die ganz davon absieht, dass und zu welchem Zweck die Leute für Lohn arbeiten, Sparren, Gewinne machen, Geld anlegen etc. Auf diese selbstgeschaffene Inhaltslosigkeit kommt es dem Ökonomen aber offensichtlich an. Er benutzt das Verhalten als Appellationsinstanz: Er will die Ausgaben A als Funktion des Einkommens Y darstellen. Aber weil er für diesen Zusammenhang auch nicht die Spur eines Arguments hat, eröffnet er mit dem Hinweis auf das Verhalten der Leute eine Möglichkeit, sich bei dieser Funktion etwas zu denken. Irgendwie, soll man sich vorstellen, könnte es ja sein, dass die Leute dafür sorgen, dass aus dem Y ein A wird - wenn schon das Y selber kaum etwas bewegen kann. Und mit demselben Irgendwie ist auch für jeden die Brücke zu seinen eigenen alltäglichen Aktionen geschlagen: Wenn bei Muttern daheim Einnahmen und Ausgaben zusammenhängen, wird's in der großen Welt wohl ähnlich sein.

„Die Höhe der Ausgaben ... hängt von der Höhe des Einkommens ... ab.... Die gesamtwirtschaftliche Ausgabenfunktion lautet daher A(t) = A(Y(t)).“ (Münnich,101)

Wir bemerken am Rande, dass die Sache mit dem Verhalten jetzt erst mal wieder rum ist. Die Wirtschaftssubjekte haben ihre Schuldigkeit getan. Ab jetzt hat die Mathematik das Wort, und der Gebrauch von deren Symbolik stiftet mindestens soviel Vertrauen wie der Appell an das ungebildete Vorstellungsvermögen.

Schöpfung einer Funktion aus dem Nichts

Weil die Welt, zu der sich der Ökonom emporgearbeitet hat, aus Größen besteht, ist die Inkarnation des Abhängigkeitsgedankens eine mathematische Funktion. Eine solche schreibt er an - oder? Mitnichten. Was hier mit A = A(Y) notiert wird, ist nicht eine bestimmte Funktion. Die Buchstaben stehen nicht wie sonst in der Mathematik für etwas wohl Definiertes, beispielsweise einen Rechenausdruck, der den Zusammenhang zwischen den Größen A und Y tatsächlich angeben würde. Die Symbole, so solide und für den Laien ehrfurchtsheischend sie auch aussehen mögen, stehen dafür, dass der hierher gehörige Rechenausdruck erst noch gefunden werden muss: Was diese Zeichen bezeichnen, weiß noch kein Mensch - und trotzdem stehen sie da.

„Die Art der Beziehungen, die auf der allgemeinen Schreibweise der Gleichung nicht ersichtlich ist, muss im konkreten Fall genauer angegeben (oder spezifiziert) werden.“ (Stobbe, 5)

Die Frage, welche Funktion die Funktion A(t) = A(Y(t)) eigentlich sein soll, zeigt, dass er mit letzterer nicht ein Gesetz der Realität ermittelt hat, sondern Gesetzmäßigkeiten konstruiert nach dem aberwitzigen Prinzip: Erst denke ich mir eine Sache aus -,das Verhalten der Wirtschaftssubjekte ist (irgend)eine Funktion' -, und dann denke ich mir auch noch aus, um welche es sich dabei handeln soll. Schon drollig, wie der Ökonom diese Verdrehung selbst kommentiert: „Allgemein“ nennt er den Vorsatz, den Größen einen Zusammenhang zu verpassen, und die Forderung nach „Konkretheit“ steht dann dafür, sich die Ausgestaltung vorzubehalten. Das geht z.B. so:

„Wenn wir aber sowieso eine solche Stilisierung A vornehmen müssen, dann ist es zweckmäßig, diese so einzurichten, dass sie alle wünschenswerten mathematischen Eigenschaften aufweist, die keine Verfälschung der ökonomischen Aussage herbeiführen.“ (Münnich, 39)

Ganz unverblümt propagiert der Volkswirt, dass Wissenschaft sich beim Stilisieren keinen Zwang anzutun braucht. Zwar weiß er nicht, wie die Funktion ausschaut, aber wünschen tut er sich halt eine lineare Funktion. Und wo ein Wille ist, ist auch ein Weg, sich eine solche aus dem Nichts zu erschaffen:

„Naturgemäß kann man ... jede Funktion ... durch eine Gerade anpassen.“ (Münnich, 39)

Was will er eigentlich an was anpassen? Ausgerechnet eine Funktion, die er nicht kennt, also die unbekannte Kurve an seine gewünschte und deshalb als sinnvoll bezeichnete lineare Funktion:

„wir gelangen somit zur Gleichung A(t) = a + bY(t).“ (Münnich, 102)

Frisch erfunden und schon interpretationsbedürftig

Angesichts der Genese dieser Gleichung ist der Wunsch des Ökonomen sehr verständlich, zu erklären, was sie nun überhaupt sagen soll.

„Den ersten Summanden a der rechten Seite der Gleichung bezeichnen wir als die autonomen Ausgaben, um dadurch zum Ausdruck zu bringen, dass dieser Teil der Ausgaben von der Höhe des Volksein-kommens unabhängig ist.“ (Münnich, 102)

Drollig sind diese autonomen Ausgaben klein a schon: Herr Münnich vertraut darauf, dass sich niemand mehr so genau an den Kern seiner Konstruktionsabsicht erinnert - nämlich dass er A als abhängig von Y darstellen wollte. Deshalb führt er hier eine autonome Ausgabenkomponente ein - und sagt selber noch, dass „autonom“ in schlichtem Deutsch unabhängig bedeutet. Und dieses kleine a soll explizit größer als 0 sein. Dem Normalverbraucher wird damit zwar das kleine Kunststück abverlangt, auch noch bei Y = 0, also bei Null Einkommen munter a DM „autonom“ zu verpulvern. Diesen Unsinn gibt der Ökonom durchaus zu. Allerdings verweist er diesmal nicht darauf, dass klein a ökonomisch sinnvoll, sprich in Mutterns Küchenwelt plausibel sei. Sondern er packt die Sache am genau entgegengesetzten Ende an: Klein a ist mathematisch notwendig:

„Die Höhe der autonomen Ausgaben ist daher auch nur eine aus Gründen der Darstellbarkeit der Geraden erforderliche, rein fiktive Größe.“ (Münnich, 102)

Das ist eine glatte Lüge: „Darstellbar“ als Gerade wäre natürlich die Funktion A = a + bY für a = O genauso gut. Dann handelte es sich bloß dummerweise um eine Gerade, die durch den Nullpunkt (Ursprung) des Koordinatensystems geht. Und eine solche Gerade will Münnich nun mal nicht haben. (Aus ähnlichen guten Gründen setzt er einige Einschränkungen über die Größe von b in die Welt.)

Warum nur?

Wie immer, wenn es in der Wissenschaft unmotiviert zugeht, sind die höheren Motive schon fast mit den Händen zu greifen. Münnich hat nämlich noch eine 2. Gerade in petto und möchte, dass beide zusammen einen wunderschönen Schnittpunkt ergeben. Dieser Schnittpunkt soll genau der Punkt sein, den die Wirtschaft letztendlich annimmt - wär ja auch blöd, wenn man nur Gleichungen und Geraden hätte, die nicht gänzlich festlegten, was genau bei der Wirtschaft rauskommt. Die Gleichung, um die es sich handelt, heißt A = Y. Diese Gleichung bezeichnet Münnich als „buchhalterisch“, was besagen soll, dass so und nur so die Wirtschaft mit ihren vielen Größen ins Reine kommt. Es kann und darf nicht sein - will Münnich damit sagen -, dass von dem schönen Y etwas übrig bleibt oder mehr A zustandekommt, als gewesen ist. In der Tat: Auch wir können uns nur schwer vorstellen, wo ein übriggebliebenes Y sich in der Welt aufhalten sollte - oder an welcher Stelle andererseits ein zuviel ausgegebenes A ein Loch gerissen hätte. Aber ganz und gar nicht teilen wir die ideologische Vorstellung, die hier mit einer Gleichung wissenschaftliche Formen angenommen hat. Die Vorstellung nämlich, dass die Wirtschaft ein wohlgeordnetes Gefüge von Größen, ein ewiger Kreislauf, ein Gleichgewicht sei - oder wie die ganzen Bilder des Füreinander oder der Harmonie alle heißen mögen.

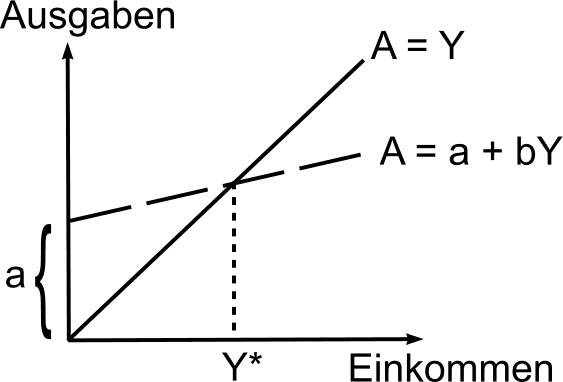
Die Nutzanwendung dieser sog. Gleichgewichtsbedingung besteht selbst-redend darin, einen Gleichgewichtspunkt festzulegen - und das geht so:

„Zur Berechnung des Gleichgewichtseinkommens setzt man Gleichung l in Gleichung 2 ein und erhält Y(t) = a + bY(t), ... eine Bestimmungsgleichung für die Größe des Gleichgewichtswertes des Volkseinkommens, den wir als

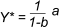
berechnen.“ (Münnich, 103)

Das Ziel des Ökonomen, seine Idee eines Gleichgewichtsvolkseinkommens, d.h. eines Punktes, wo die Wirtschaft in Ordnung geht, mathematisch vorstellbar zu machen, hat er mittels des Betrugs erreicht, seine Verhaltensgleichung mit den „Parameterwerten“ a ≠ 0 und 0 < b < 1 zu präparieren. Ohne diese methodische Vorschrift an seine eigene Gleichung, die genau diese Werte von sich aus ganz und gar nicht notwendig macht, wär's Essig gewesen mit dem Schnittpunkt. Ganz unverfroren nennt er diese seiner Beweisabsicht entsprungenen Voraussetzungen der Konstruktion des Schnittpunkts eine „Schlussfolgerung“ (S. l03) aus diesem - als würden sie sich quasi als mathematisches Gesetz notwendigerweise aus der einmal erfundenen Gleichung ergeben.

Und betrachtet man rückblickend noch mal beide Gleichungen gemeinsam, so zeigt sich der allerdickste Pferdefuß der ganzen Ableitung:

Die sog. buchhalterische Identität Y = A sollte ausdrücken, dass A nie und nimmer einen anderen Wert annehmen kann als eben Y. Die andere, die sog. Verhaltensgleichung, sollte deshalb immer gelten, weil er sie empirisch gewonnen haben will. Nur: Wenn die Lösung Y* der einzige Wert ist, der die beiden Gleichungen simultan erfüllt, so heißt das eben, dass die beiden Gleichungen für alle anderen Werte nicht miteinander zu vereinbaren sind. Die Werte von Y, die die Gleichungen, jede für sich genommen, beschreiben, sind also ideeller Natur. Und wenn die buchhalterische Gleichung A = Y - laut Definition - immer erfüllt sein muss, kann die andere, außer bei Y* nie erfüllt sein. Sie ist also der Unsinn einer „Gesetzmäßigkeit für das Ausgabeverhalten“, das in dieser Form in der Realität gar nicht vorkommen kann. Und es muss gelogen sein, dass die Ökonomen den Verlauf der ganzen Geraden - wie sie nicht müde werden zu beteuern - durch Beobachtung in der Realität gefunden haben. Deshalb wird in manchen Ökonomiebüchern diese Gerade auch nur gestrichelt gezeichnet, was ausdrücken soll, dass sie - übrigens die einzige empirische Gerade - eigentlich gar nicht da ist. Das ist aber leider sehr fatal. Fatal für den Schnittpunkt. Es gibt keine Gerade mehr, die ihn bilden könnte, also auch keinen Schnittpunkt, also auch kein Gleichgewicht.

Fazit:

Herhalten muss die Mathematik, um die ideologische Botschaft des Ökonomen in die Welt zu bringen: die Wirtschaft ist ein Mechanismus. Sie besitzt einen inneren Zusammenhang, der immer aufgeht, und die Leute bringen mit dem, was sie wollen, genau jenen Zusammenhang hervor - ihr Wille passt zum Mechanismus wie die Faust aufs Auge. Ihre Entscheidungsfreiheit ist mit der Notwendigkeit in Übereinstimmung, lautet die Moral des Gleichungssystems. Diese verkehrten Ideen des Volkswirts erhalten dadurch Glaubwürdigkeit, dass er sie mathematisch fasst: Eine Welt, in der das Zusammenwirken gegensätzlicher Zwecke erzwungen wird, soll durch die Erfindung seiner mathematischen Gesetzmäßigkeiten als Sachgesetz und mathematisch wohlgeordnet denkbar sein. Die Berechenbarkeit soll der Welt der Wirtschaft die unwidersprechliche Vernunft verleihen und sie darin als ebenso unanfechtbar wie die Natur darstellen, deren Gesetze tatsächlich unabhängig vom Wollen Objektivität und mathematische Gestalt haben.

Beispiel 3: Der mikroökonomische Optimierungsgedanke oder: Jedes Wirtschaftssubjekt berechnet immer sein Bestes

Bei allem, was der Mensch so tut und treibt - Versicherungspolicen kaufen, Geige spielen oder einfach einen Nagel in die Wand schlagen -, kann er seine Sache gut oder schlecht machen. Das Prädikat „gut“ verdient er, wenn er das, was die jeweilige Tätigkeit ausmacht, richtig hinkriegt. Das Prädikat „schlecht“ verdient er, wenn er den Anforderungen seines Tuns nicht gehörig nachkommt. Das kann an äußeren Hindernissen, an Unvermögen oder an Voreingenommenheit durch andere Zwecke liegen. Aber egal. Was gut ist und was schlecht, bemisst sich jedenfalls an der auszuführenden Tätigkeit; „gut“ fällt völlig damit zusammen, dass sie ihrer Bestimmung gemäß und ungestört ausgeführt wird. Man nimmt sich deshalb auch nicht vor, erstens einen Nagel in die Wand zu schlagen und zweitens dies möglichst gut zu tun. Der eine Vorsatz reicht völlig aus, in ihm ist alles enthalten.

Die Mikroökonomie behauptet nun, das Verhalten der Wirtschaftssubjekte sei damit zu erklären, dass sie ihre Sache möglichst gut machen wollen: Was auch immer sie tun, sie optimieren, wie der wissenschaftliche Ausdruck lautet. Und aus diesem Prinzip soll sich ein Verständnis der jeweiligen Tätigkeit insgesamt ergeben.

Falsch ist dieser Optimierungsgedanke, weil er etwas zum allgemeinen Inhalt wirtschaftlicher Tätigkeit macht, was, wie wir gesehen haben, überhaupt keine Inhaltsbestimmung von irgend etwas auf der Welt sein kann. Was die einzelnen Tätigkeiten ausmacht - arbeiten gehen, Aktien kaufen etc. -, wird so ganz einfach unterstellt; ihre Spezifik wird keiner Bestimmung und weiteren Erklärung für würdig befunden. Umgekehrt sollen sich diese ökonomischen Tätigkeiten als Beispiele, Sonderfälle und Einkleidungen aus dem in dieser Abstraktheit widersinnigen und inhaltsleeren Tun begreifen lassen, das darin besteht, es gut zu machen.

Um seine falsche Abstraktion, also das „gut“-machen als selbständige Tätigkeit, in einen wissenschaftlichen Gegenstand umzumünzen, beruft sich der Mikroökonom auf die Mathematik, und zwar denkt er insbesondere an die folgende Abteilung: Die Mathematik besitzt Verfahren, sogenannte Extremwerte, also Maxima, Minima, von Funktionen auszurechnen.

Jeder, der eine höhere Schule besucht hat, kennt die Grundzüge dieser Technik unter dem Stichwort „Kurvendiskussion“, und er hat sie sicher auch schon angewendet gesehen. Beispielsweise, um in der Physik bei Wurfparabeln den höchsten Punkt oder den Winkel größter Reichweite auszurechnen. Bloß: Wenn die Mathematik so ganz allgemein von Extremwertaufgaben und Techniken ihrer Lösung handelt, dann ist das noch lange nicht die falsche Abstraktion der Optimierung, auf die die Ökonomen hinauswollen. Genauso wie zum Rechnen mit seinen Regeln und Techniken Zahlen gehören, so gehören zur Kurvendiskussion ordentliche Kurven bzw. die sie beschreibenden Funktionen. Das sind die Gegenstände der Mathematik, abstrakte, aber genau bestimmte Dinge, und sie haben mit der Vorstellung eines „es möglichst gut machen wollen“ nichts gemein.

Um nun die Sache der Mathematik als die eigene auszugeben, behauptet der Mikroökonom als nächstes, dass die von ihm betrachteten Wirtschafts-tätigkeiten darin bestünden, für eine variable Größe - die sogenannte Zielfunktion - ein Maximum zu finden. Egal, ob Arbeiten, Einkaufen, Geld anlegen - dass hier lauter Extremwertaufgaben vorliegen, verkündet die Ökonomie als hochwissenschaftlichen Aspekt der Sache.

Wie dumm diese Behauptung ist, sieht man vielleicht am besten am Beispiel einer Wirtschaftstätigkeit, die tatsächlich ein quantitatives Kriterium für gutes bzw. schlechtes Gelingen hat. Wenn einer an der Börse spekuliert, will er einen Gewinn, einen Überschuss in Geld machen. Und Geld als Zweck hat es nun mal an sich, dass man nie genug davon kriegen kann. Die Vorstellung, dass so ein Spekulant - oder ein Kapitalist überhaupt - nach einem Gewinnmaximum strebt, ist aber eben deshalb grundfalsch: Maßlosigkeit ist das Prinzip der Profitmacherei, und nicht Streben nach einem maximalen Gewinn. Und sowenig er vorhat, eine ganz bestimmte Gewinnhöhe anzusteuern, sowenig hat er auch eine Funktion oder Kurve, die diesen „richtigen“ Punkt zu ermitteln gestattete. Schließlich heißt die Sache „Spekulation“ und nicht „Ausrechnen“, wo es um Kauf und Verkauf der richtigen Papiere zum richtigen Zeitpunkt geht. Hat da der Verlierer vielleicht vergessen, dass er optimieren wollte? Oder hat er in der Lotterie des Schicksals die falsche Kurve verpasst gekriegt?

Lieber einen Mercedes als noch einen BMW

Die Fortsetzung der Theorie besteht deshalb notwendigerweise in der Neuschöpfung ihrer Gegenstände:

„Die von den betrachteten Wirtschaftssubjekten in der Realität verfolgten Ziele sind nur Schwer zu fassen und nicht eindeutig formulierbar ... Man kann allgemein von der Sorge um das Wohlergehen der Familienmitglieder und somit davon ausgehen, dass der Haushalt jeweils das ihm am günstigsten erscheinende Gütersortiment auswählen wird, das er mit dem zur Verfügung stehenden Budget kaufen kann ... In der älteren Literatur wurde statt der Annahme der Wahl des bestmöglichen Gütersortiments das Ziel der Maximierung des Nutzens--im Sinne eines Maximums an erreichter Bedürfnisbefriedigung-- formuliert. Theoretiker wie Gossen ... strebten an, den Nutzen der Haushalte in bestimmten Nutzeneinheiten zu messen ... Deshalb spricht man bei diesem Ansatz von einer kardinalen Nutzengröße. Diese Bestrebungen haben nicht den erhofften Erfolg gezeitigt; man hat allgemein in der Haushaltstheorie zurückgesteckt und beschränkt sich darauf, Nutzenvergleiche anzustellen ... Man hat sich auf ein ordinales Nutzenkonzept zurückgezogen, behält jedoch weiterhin dass Ziel der Maximierung des Nutzens bei, wiewohl dieser nicht in absoluten Größen gemessen wird ... Am Ergebnis der Analyse ändert sich dadurch gegenüber den traditionellen Ansätzen nicht." (Böventer, 11-12)

Natürlich sind die Ziele der Wirtschaftssubjekte überhaupt nicht schwer zu fassen. Die Leute werden schon wissen, was sie wollen, und der Ökonom bräuchte sie z.B. nur zu befragen. Und natürlich weiß er auch ohne diese Mühe schon, wie die Antworten aussehen würden - aber eben dies stört ihn: „in der Realität“ gibt's mannigfache Zwecke und Bedürfnisse, aber weit und breit keine „eindeutige“ Zielfunktion. Diese richtig zu „formulieren“, ist deshalb die Aufgabe der Wissenschaft.

Für den „Haushalt“ - die Ökonomen-Stilisierung der einkaufenden und konsumierenden Menschheit - heißt die einzuführende Größe „Nutzen“. Natürlich unterscheidet ein Konsument in der Vielzahl der nützlichen Dinge, was seinen speziellen Bedürfnissen dient und was nicht, oder was ihm dann im Einzelfall besser oder schlechter gefällt. Und die Schranken seines Geldbeutels zwingen ihn laufend dazu, beim Einkaufen auf den einen durchaus gewünschten Gegenstand zu verzichten, damit er sich den anderen leisten kann. Aber weder die Unterschiede, die das Bedürfnis macht, noch der Verzicht, den das liebe Geld einem aufnötigt, lassen sich durch eine Größe namens „Nutzen“ erklären, die mehr oder weniger vorhanden sein soll. Was sollte das denn auch heißen, dass ein Auto mir mehr Nutzen brächte als eine Reise nach Teneriffa? Entweder ich will gar nicht dorthin. Oder ich hätte gerne beides, aber muss mich aus Geldgründen zwischen diesen so gar nicht vergleichbaren Dingen entscheiden. Da mag ich dann sogar Gründe haben, das Auto zu wählen (und in der Regel sind solche Gründe wiederum aus der Not geboren, also dass ich z.B. das Auto für meine täglichen Verpflichtungen brauche). Aber ganz gewiss lasse ich das eine Bedürfnis nicht deshalb unbefriedigt, weil mir das andere ein „Mehr an Befriedigung“ verschafft. Schließlich ist Hunger auch nicht schlimmer als Durst und umgekehrt.

Die Modernisierung der Nutzentheorie: ein Optimum von nichts Bestimmtem

Diese idiotische Vorstellung von miteinander vergleichbaren Nutzenmengen bzw. Graden der Befriedigung, die ganz verschiedene Konsumartikel gewähren, ist absolut notwendig, aber auch völlig ausreichend für die Verwandlung des Einkaufens in ein Optimierungsproblem. Nichtsdestotrotz haben die Ökonomen beschlossen, diesen ihren zentralen Fehler noch zu verbessern. Zum Beispiel haben sich einige daran gestört, dass der Nutzen, weil er nicht existiert, auch nicht überzeugend gemessen werden kann. Zwar teilt der Nutzen dieses Schicksal mit sämtlichen Größen der VWL (siehe Sozialprodukt) aber diesmal sind die Ökonomen auf den Spleen verfallen, ihr Programm unter ausdrücklichem Verzicht auf ein Maß des Nutzens durchziehen zu wollen. Die Grundidee ist die folgende: Man kann eine Gruppe von Leuten sich nach ihrer Größe aufstellen lassen. Man kann diese Leute aber auch in alphabetischer Reihenfolge aufstellen lassen. In beiden Fällen kann man dann den ersten in der Reihe vortreten lassen. Und diese Tatsache, dass eine lineare Ordnung auch ohne Größenvergleich, sondern eben nach einem anderen Prinzip herstellbar ist, hat Ökonomen zu dem Einfall beflügelt, ihr Optimierungsprogramm ohne Nutzengrößen und deren Vergleich durchzuziehen: Nutzenmaximierung sei hinfort so verstanden, dass die oberste Position in einer Rangordnung der Güter gewählt wird.

Die Frage, wie ein Konsument diese Rangordnung herstellen soll, wollen wir lieber nicht stellen. Die VWL hält sich für einen Ausbund an wissenschaftlicher Redlichkeit, wenn sie darüber keine Annahmen macht. Aber dass diese Rangordnung in jedermanns Hirnkasten existiert, das möchte sie in ihrer wissenschaftlichen Redlichkeit schon annehmen.

Für weit verdienstvoller hält sie dann die Frage, wie man denn nun von der Vorstellung einer Rangordnung den Weg zurück zu den bewährten Kurvendiskussionen der Mathematik findet, auf die man es ja eigentlich abgesehen hat.

Wir rufen sicher kein Erstaunen hervor, wenn wir hier zusammenfassend mitteilen, dass dieser Weg mit geistigen Klimmzügen gepflastert ist, dass er von Studenten der Mikroökonomie kaum jemals komplett verstanden wird und dass selbst namhafte Lehrbuchautoren daran scheitern, ihn ihren eigenen Qualitätsmaßstäben entsprechend darzustellen. (z.B. Böventer S. 6l: „Das Konzept stetiger Präferenzen ist nicht ganz einfach, und wir werden deshalb nicht eine allgemeine und formal präzise Definition dieses Begriffs entwickeln ...“) Und natürlich handelt es sich um lauter Fehler. Der wichtigste sei hier mitgeteilt: Wenn wir in unserem Beispiel die Leute in alphabetischer Reihenfolge antreten lassen, können wir ihnen anschließend auch Platzziffern verpassen: Amalie = l, Anselm = 2, Anton = 3 usw. usf. Heureka, schreit der Ökonom, wir sind zurück auf quantitativem Gebiet!

Bloß: Solche Platzziffern sind nur eine alternative Manier, die betrachtete Rangordnung auszudrücken oder festzuhalten. Man benutzt den Umstand, dass die Zahlen auch eine Ordnung haben, man stellt gewissermaßen einen Vergleich an. Aber deswegen kann man sich noch lange nicht alle Qualitäten der Zahlen zueigen machen. Zahlen geben ein Mehr oder Weniger an  aber was sollte es heißen, dass Anselm mehr ist als Amalie und Anton noch mehr? Und mit Zahlen kann man rechnen - aber was sollte es heißen, dass der Anselm zweimal die Amalie ist usw.?

Diesen Unterschied gibt der Ökonom mit seiner protzigen Differenzierung zwischen „kardinalen“ und „ordinalen“ Größen selber zu - aber nur soweit er scharf drauf ist, das leidige Problem mit der Nutzenmessung zu umgehen. Und kaum hat er für den wissenschaftsstrategischen Vorteil bloß „ordinaler“ Größen genügend Reklame gemacht, vergisst er ganz einfach den eben noch so wichtigen Unterschied und behandelt seine Platzziffern wie stinknormale kardinale Größen. Dieses Unterscheiden und anschließende Vergessen ist das Geheimnis des letzten Satzes im Zitat: „Am Ergebnis der Analyse ändert sich dadurch gegenüber den traditionellen Ansätzen nichts.“

Also: Erst soll man glauben, dass die Konsumenten den Gütern keineswegs einen „Nutzen“ verschiedener Größe verpassen, sondern nur Indizes oder Platzziffern gemäß einer Rangordnung - und dann soll man auf einmal glauben, dass es eine stetige, differenzierbare und mit sonstigen mathematischen Annehmlichkeiten ausgestattete „Nutzenfunktion“ gibt die die Größe des Nutzens aus den Quanta der betrachteten Güter zu berechnen gestattet.

Also erst soll der Konsument bloß eine Einkaufstüte mit 20 Zigaretten und zwei Pfund Haferflocken besser finden als eine Einkaufstüte mit 100 Zigaretten und einem Pfund Haferflocken. Aber dann soll er auf einmal eine Funktion (Beispiel Böventer S. 89) u = x₁ x₂ haben, wobei u = der Nutzen, x₁ = die Zigaretten und x₂ = die Haferflocken sein sollen. Dass sich jetzt natürlich wunderschöne Extremwertaufgaben stellen und lösen lassen, glauben wir ja gerne. Aber dass sich diese wissenschaftliche Leistung einem Beschiss verdankt, ist selbst im Resultat noch überdeutlich: einerseits soll der Nutzen eine Zahl sein, bei der man sich nichts denken dürfen soll; andererseits aber hat der Nutzen jetzt auf einmal eine Dimension gekriegt, nämlich Stück Zigaretten mal Pfund Haferflocken, ist also eine sehr substanzielle, wenn auch nicht unbedingt schmackhafte Sache geworden. Und was ist, wenn unser Konsument seine Nutzenfunktion zum neuen Jahr auf u = x₁ x₂² geändert hat? Dann ist Nutzen auf einmal Zigaretten mal Haferflocken im Quadrat und somit eine ganz andere Sache als im Jahr zuvor!

Die Wissenschaft hat festgestellt: Alles bestens auf der Welt!

An den theoretischen Anstrengungen der Mikroökonomie ist der Anspruch unübersehbar, dass man doch ausrechnen können müsse, was die Wirtschaftssubjekte tun und treiben. Wenn aber jetzt, um beim Beispiel Haushalt zu bleiben, der Käufer aus dem Supermarkt tritt, weiß dann die Mikroökonomie, was in seiner Plastiktüte ist? Mitnichten. Denn die von der Theorie mit soviel Mühe erschlossenen Rechenmethoden funktionieren nur, wenn die eingangs postulierte Nutzenfunktion bekannt ist. Und das wird noch nicht einmal der größte Angeber unter den Ökonomen behaupten.

Also reduziert sich der ganze Formelkram, der doch eigentlich zum Rechnen da ist, auf einen Kommentar zum Weltgeschehen. Den Kommentar nämlich, dass der Käufer ganz gewiss das innerhalb seiner finanziellen Schranken für ihn günstigste Warensortiment erworben hat.

Einerseits ist dieser Kommentar die albernste Tautologie, die man sich vorstellen kann. Denn natürlich kauft sich keiner Rothändle statt Marlboro, wenn er lieber Marlboro hätte.

Das ist genauso eine Schlaumeierei, wie wenn ein Meteorologe nicht eine Wetterprognose abgeben, sondern sich auf die Auskunft beschränken würde, es käme immer das Wetter, das sich „durchsetzt“.

Andererseits wird mit dieser Pseudo-Bescheidwisserei für eine Interpretation des Kaufens gesorgt, die es in sich hat. Denn beim Einkaufen ist man mit der Tatsache konfrontiert, dass die Gegenstände des Bedürfnisses zwar die Kaufhäuser füllen, aber keineswegs für einen selbst bestimmt sind. Als Waren haben die nützlichen Dinge die Bestimmung, ihrem Besitzer Geld einzubringen. Der Kapitalismus produziert massenhaft Reichtum und trennt ihn von den bedürftigen Individuen. Das mag man einen Widerspruch nennen oder einfach Scheiße. Aber die Ökonomie verwandelt dies höchst ungemütliche und keineswegs notwendige Verhältnis (es wird ja genug produziert) in ein ewiges Menschheitsproblem, das darin beistehen soll, aus jeweils beschränkten Gegebenheiten das Beste zu machen. Und so gesehen geht eine Welt voll Armut und Gewalt schon ziemlich in Ordnung.

Beweisbar ist diese apologetische Interpretation natürlich nicht. An die Stelle eines Beweises aber tritt jetzt die Vorschrift, dass sich solche Weltanschauung nach allen selbstgesetzten Regeln und Schikanen der Wissenschaft durchführen läßt.

Solche Theoretiker fragen sich nicht, was der Kauf von Waren ist, sondern wie sich die vorgefasste gute Meinung davon, der Optimierungsgedanke, immer exakter ausbauen lässt. Deshalb lassen sie sich erst einen ganz exakten Nutzen einfallen. Deshalb sind sie so frei, diese Nutzenfunktion als nächstes durch abstrakte Ordnungen und Hierarchien noch viel exakter zu untermauern. Und deshalb sind diese Brüder auch so scharf auf Mathematik.

Zahlen, Funktionen und Gleichungen sind nicht nur die Insignien und Schaustücke der Gelehrsamkeit, sondern in der Tat auch die adäquaten Ausdrucksmittel der Botschaften, auf die Ökonomen scharf sind: lauter Sachgesetze und Notwendigkeiten, lauter Berechnungsmöglichkeiten und Gleichungen, die aufgehen - mit einem Wort, die Welt des Klassen-gegensatzes und der Konkurrenz geht in Ordnung.

Verwendete Literatur

Henrichsmeyer, Einführung in die Volkswirtschaftslehre, Stuttgart l978

Böventer, Einführung in die Mikroökonomie, 4. Aufl., München l985

Münnich, Einführung in die empirische Makroökonomik, Berlin l982

Bartling, H.; Luzius, Grundzüge der Volkswirtschaftslehre, 4. Aufl., München l983

Stobbe, Volkswirtschaftslehre 1, Volkswirtschaftliches Rechnungswesen, 4. Aufl., Berlin l976